Tính chất hình bình hành
Trong hình học phẳng, hình bình hành là một trong những hình tứ giác đặc biệt có vai trò nền tảng trong việc xây dựng kiến thức về hình học Euclid. Dù có thể dễ dàng bắt gặp nó trong các bài toán cơ bản, nhưng hiểu một cách thấu đáo về tính chất của hình bình hành lại mang lại nhiều giá trị hơn thế – từ việc giải toán học phổ thông đến ứng dụng trong kỹ thuật, kiến trúc, và thiết kế.
Hình bình hành là tứ giác có hai cặp cạnh đối song song. Chính đặc điểm này giúp nó sở hữu nhiều tính chất đặc biệt và là cơ sở hình thành các hình như hình chữ nhật, hình thoi hay hình vuông.
Hình bình hành ABCD
Ví dụ, với tứ giác ABCD nếu AB // CD và AD // BC thì ABCD là hình bình hành. Đây được xem là dạng mở rộng của hình chữ nhật nhưng không yêu cầu bốn góc vuông.
2.1 Cặp cạnh đối có hướng song song và cùng chiều dài
Trong một hình bình hành, hai cạnh nằm đối diện luôn có chiều dài bằng nhau và chạy song song, tạo nên tính đối xứng đặc trưng của loại hình tứ giác này.
Tính chất hình bình hành: Cặp cạnh đối cùng chiều dài và song song
2.2 Cặp góc đối có số đo bằng nhau
Hai cặp góc đối trong hình bình hành luôn bằng nhau về độ lớn, nghĩa là ∠A = ∠C và ∠B = ∠D. Tính chất này thể hiện sự cân bằng về góc và thường được vận dụng để giải các bài toán liên quan đến đo lường và chứng minh trong hình học phẳng.
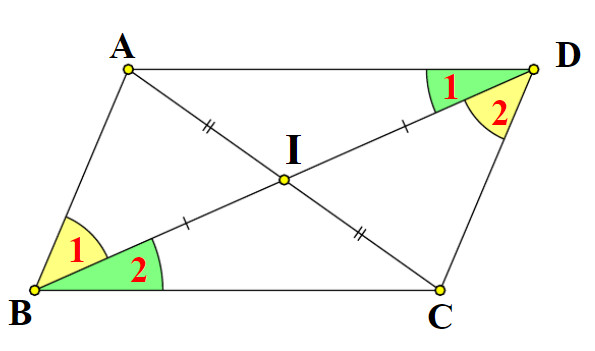
2.3 Hai đường chéo cắt nhau tại trung điểm
Một đặc điểm đáng chú ý trong hình học của hình bình hành là hai đường chéo không chỉ giao nhau, mà còn chia nhau thành hai đoạn có độ dài bằng nhau tại điểm cắt đó.
2.4 Tổng hai góc kề bằng 180 độ
Đây là tính chất mở rộng của hình tứ giác nội tiếp hình tròn, nhưng với hình bình hành, nó luôn đúng: Tổng hai góc liền kề bất kỳ đều bằng 180°, do hai cạnh kề song song với nhau.
2.5 Mỗi đường chéo của hình bình hành tạo ra hai tam giác có kích thước bằng nhau
Một đường chéo bất kỳ sẽ chia hình bình hành thành hai tam giác có diện tích và các yếu tố tương đương nhau – từ độ dài cạnh đến số đo góc. Tính chất này rất quan trọng trong việc chứng minh sự bằng nhau hoặc tương đương trong các bài toán hình học.
>> Tham khảo: Tính chất hình thoi
Hình chữ nhật là một trường hợp riêng của hình bình hành, nơi mà bốn góc đều là góc vuông.

Hình chữ nhật cũng là hình bình hành
Hình thoi là kiểu hình bình hành đặc biệt có độ dài bốn cạnh bằng nhau.
Hình vuông là sự kết hợp đồng thời giữa hai yếu tố: góc vuông của hình chữ nhật và cạnh bằng nhau của hình thoi – tức là hình bình hành vừa vuông vức vừa đều cạnh.
Nhờ kế thừa cấu trúc cơ bản của hình bình hành, những hình này vẫn giữ được các tính chất chung như: hai cặp cạnh đối song song và bằng nhau, hai góc đối bằng nhau, và các đường chéo giao nhau tại trung điểm của mỗi đường. Tuy vậy, mỗi loại hình vẫn sở hữu những nét đặc trưng riêng, làm nên sự khác biệt rõ ràng và dễ nhận biết giữa chúng.
Hình bình hành không chỉ xuất hiện trong các bài toán hình học, mà còn có mặt rộng rãi trong thực tiễn đời sống và kỹ thuật:
4.1 Trong kiến trúc và xây dựng
Nhiều thiết kế mái nhà, cửa sổ, sườn mái hay mặt cắt chịu lực của cầu đều ứng dụng hình bình hành để đảm bảo tính cân bằng và phân bổ lực đều. Việc tận dụng tính chất của hình bình hành giúp công trình bền vững, chịu lực tốt mà vẫn giữ được yếu tố thẩm mỹ.
4.2 Trong kỹ thuật cơ khí
Trong các hệ thống truyền động (ví dụ máy ép, máy cắt), khung hình bình hành thường được sử dụng để truyền lực ổn định từ một điểm đến điểm khác. Cơ cấu chuyển động theo nguyên lý hình bình hành giúp tạo ra các quỹ đạo ổn định và lặp đi lặp lại.
4.3 Trong đồ họa và thiết kế
Các phần mềm thiết kế 2D, 3D đều sử dụng thuật toán dựng hình dựa trên các đơn vị hình học cơ bản – trong đó hình bình hành đóng vai trò quan trọng để tạo ra phối cảnh và chiều sâu.
4.3 Trong giáo dục STEM
Việc giảng dạy tính chất hình bình hành không chỉ nhằm giúp học sinh giải toán, mà còn là cơ sở để phát triển tư duy logic, khả năng lập luận hình học và làm quen với các khái niệm không gian – kỹ năng then chốt trong khoa học, kỹ thuật, và công nghệ.
Trong quá trình học hình học phẳng, một dạng bài tập quen thuộc là xác định xem một tứ giác bất kỳ có phải là hình bình hành hay không. Để làm điều này, học sinh cần biết cách sử dụng linh hoạt các đặc điểm đặc trưng của hình bình hành – những yếu tố có thể dễ dàng kiểm tra từ hình vẽ hoặc các dữ kiện bài toán cung cấp.
Một phương pháp đơn giản và hiệu quả để nhận biết hình bình hành là dựa vào mối quan hệ giữa các cạnh. Nếu một tứ giác có một cặp cạnh đối vừa song song vừa có độ dài bằng nhau, thì hình đó chính là một hình bình hành. Đây là dấu hiệu kết hợp giữa song song và bằng nhau – hai yếu tố đặc trưng trong tính chất hình bình hành thường gặp.
Ngoài ra, việc quan sát các cặp cạnh đối song song cũng là một cách làm phổ biến. Khi cả hai cặp cạnh đối của tứ giác cùng song song, thì không cần kiểm tra thêm – đó là một hình bình hành. Cách tiếp cận này giúp rút gọn quá trình lập luận, nhất là trong các bài toán có hình ảnh minh họa rõ hoặc tọa độ cụ thể.
Một dấu hiệu đặc biệt khác ít được chú ý hơn là xét hai đường chéo của tứ giác. Nếu hai đường chéo cắt nhau đúng tại trung điểm mỗi đường, ta có thể kết luận đó là hình bình hành. Đây là một trong những tính chất hình bình hành ít phổ biến trong giảng dạy sơ cấp, nhưng lại rất mạnh trong việc giải quyết các bài toán phức tạp hơn hoặc có sử dụng phép đối xứng, trung điểm hay đường trung bình.
Hiểu và vận dụng đúng các tính chất hình bình hành không chỉ giúp học sinh tiết kiệm thời gian làm bài mà còn phát triển khả năng tư duy không gian và kỹ năng lập luận logic. Với nền tảng này, người học có thể tiếp cận hiệu quả hơn với các chủ đề liên quan như hình học tọa độ, vector, Phương pháp còn được ứng dụng hiệu quả trong thực tiễn như thiết kế công trình và cơ khí kỹ thuật
Tóm lại, muốn chứng minh một tứ giác là hình bình hành, hãy tập trung vào ba yếu tố chính: mối quan hệ giữa các cạnh, sự song song của các cặp cạnh, và cách các đường chéo tương tác với nhau. Chỉ cần nắm chắc những nguyên tắc này, bạn đã có trong tay một công cụ mạnh mẽ để chinh phục mọi dạng bài hình học liên quan đến loại tứ giác đặc biệt này.