Tính chất hình thoi
Trong thế giới hình học phẳng, mỗi hình tứ giác đều mang những đặc trưng riêng, tạo nên sự đa dạng và thú vị trong quá trình học tập. Hình thoi là một trong những dạng tứ giác đặc biệt đáng chú ý, sở hữu tính đối xứng nổi bật và hình dáng đơn giản nhưng ẩn chứa nhiều tính chất thú vị. Việc hiểu rõ tính chất hình thoi không chỉ giúp giải bài tập hình học hiệu quả mà còn là nền tảng để phát triển tư duy hình học không gian và ứng dụng thực tiễn.
Bài viết này sẽ giúp bạn đi sâu khám phá hình thoi từ định nghĩa đến các tính chất đặc trưng, phương pháp nhận dạng và một số ứng dụng gần gũi trong đời sống, đảm bảo hoàn toàn mới mẻ và khác biệt so với những nội dung phổ biến hiện nay trên mạng.
Trong hệ thống các tứ giác, hình thoi được định nghĩa là một hình có bốn cạnh bằng nhau, trong đó hai cặp cạnh đối song song. Hình vuông phải có góc vuông, còn hình thoi thì không cần điều đó.
Hình dạng của hình thoi
Điều này dẫn đến một đặc điểm: hình thoi là một loại hình bình hành đặc biệt, nhưng không phải hình bình hành nào cũng là hình thoi.
Đặc điểm | Hình bình hành thông thường | Hình thoi |
Độ dài cạnh | Hai cặp cạnh bằng nhau | Tất cả 4 cạnh bằng nhau |
Đường chéo | Không vuông góc | Vuông góc tại trung điểm |
Góc trong | Không vuông góc | Không cần vuông nhưng đối xứng |
Để nhận biết và làm việc với hình thoi hiệu quả, cần nắm vững các tính chất hình thoi sau:
2.1. Bốn cạnh có độ dài bằng nhau
Đây là yếu tố cốt lõi, quyết định tứ giác đó có phải hình thoi hay không. Chỉ cần đo độ dài của bốn cạnh và chúng bằng nhau, ta có thể khẳng định hình đó là hình thoi (với điều kiện nó là tứ giác lồi).
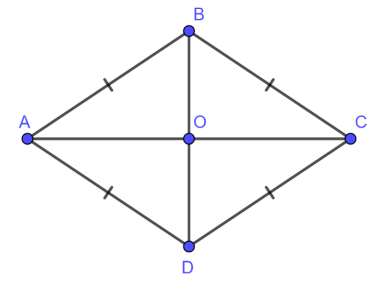
Bốn cạnh của hình thoi bằng nhau2.2. Hai đường chéo cắt nhau tại trung điểm và vuông góc
Một đặc điểm nổi bật giúp phân biệt hình thoi với hình bình hành thông thường là hai đường chéo giao nhau tại trung điểm và tạo thành một góc vuông. Điều này nghĩa là mỗi đường chéo chia hình thoi thành hai tam giác vuông bằng nhau, từ đó có thể áp dụng vào nhiều bài toán chứng minh hình học.
2.3. Đường chéo chia đôi góc tại đỉnh
Khác với hình chữ nhật, trong đó hai đường chéo chỉ cắt nhau tại trung điểm mà không ảnh hưởng đến các góc ở đỉnh, thì ở hình thoi, mỗi đường chéo lại có vai trò đặc biệt hơn...còn là đường phân giác chia đôi góc mà nó đi qua.
2.4. Các góc đối bằng nhau
Do là hình bình hành đặc biệt, hình thoi vẫn giữ được tính đối xứng về góc, tức là hai cặp góc đối diện nhau có cùng số đo. Ngoài ra, tổng hai góc kề nhau (góc ở hai đỉnh liền cạnh nhau) luôn bằng 180 độ, do đó khi biết một góc, ta dễ dàng suy ra ba góc còn lại.
>> Tham khảo: Đường cao tam giác đều
Trong các đề bài hình học hoặc toán thực hành, việc nhận diện hình thoi thường không trực tiếp, mà thông qua các dấu hiệu gián tiếp. Dưới đây là một số cách giúp bạn xác định một hình có phải hình thoi hay không:
Dấu hiệu nhận biết đầu tiên: Hình tứ giác có tất cả các cạnh có độ dài bằng nhau.→ Đây là dấu hiệu nhanh nhất và rõ ràng nhất.
Dấu hiệu 2: Một hình bình hành có hai cạnh kề bằng nhau
→ Nếu hình bình hành có thêm điều kiện này, ta có thể kết luận đó là hình thoi.
Dấu hiệu 3: Đường chéo giao nhau tại trung điểm và vuông góc
Dựa vào điều kiện trên, ta có thể xác định tứ giác là hình thoi mà không cần kiểm tra độ dài các cạnh.
Trong lĩnh vực hình học phẳng, hình thoi là một loại tứ giác đặc biệt với bốn cạnh bằng nhau và hai đường chéo vuông góc nhau, đồng thời giao nhau tại trung điểm mỗi đường. Chính nhờ sự đối xứng và tính chất hình học đặc trưng, hình thoi được sử dụng rộng rãi trong giảng dạy và kiểm tra đánh giá học sinh.
Một trong những ứng dụng thực tiễn rõ rệt nhất liên quan đến hình thoi là việc tính diện tích của nó. Phương pháp tính diện tích dựa trên mối liên hệ giữa hai đường chéo — yếu tố đóng vai trò quan trọng trong việc xác định tổng diện tích toàn phần của hình. Khi hai đường chéo được biết trước, ta có thể coi hình thoi như sự kết hợp của bốn tam giác vuông nhỏ. Từ đó, ta áp dụng công thức tính diện tích bằng cách nhân chiều dài hai đường chéo rồi chia đôi, do diện tích hình thoi tương đương với diện tích của hai tam giác vuông đối xứng nhau gộp lại. Cụ thể như sau:
Công thức chung:
Diện tích (S) = ½ × d₁ × d₂
Trong đó:
Ký hiệu d₁ và d₂ lần lượt đại diện cho chiều dài của hai đường chéo trong hình thoi.
Trong đó:
d₁ là độ dài đường chéo thứ nhất
d₂ là độ dài đường chéo thứ hai
Ký hiệu S được dùng để chỉ diện tích của hình thoi, đơn vị thường sử dụng là đơn vị vuông như cm², m², tùy theo hệ đo được áp dụng.
Ví dụ cụ thể:
Xét một hình thoi có hai đường chéo lần lượt dài 8 cm và 6 cm. Khi áp dụng công thức tính diện tích, ta thực hiện như sau:
S = ½ × 8 × 6 = 24 (cm²)
Phương pháp tính này cực kỳ đơn giản, không yêu cầu góc hay độ dài cạnh, vì đường chéo là yếu tố dễ xác định khi biết tọa độ các đỉnh hoặc thông qua mô hình hình học.
Tuy là một hình học cơ bản trong chương trình toán, tính chất của hình thoi không đơn thuần chỉ xuất hiện trên sách vở mà còn được ứng dụng rộng rãi trong nhiều lĩnh vực đời sống, từ kỹ thuật, nghệ thuật đến thiết kế hiện đại.
5.1. Thiết kế nội thất và trang trí không gian
Nhiều mẫu gạch lát sàn, trần nhà hoặc giấy dán tường sử dụng họa tiết và tính chất hình thoi để tạo chiều sâu thị giác và cảm giác cân bằng. Các đường chéo của hình thoi giúp không gian có sự chuyển động nhẹ, khiến bố cục trở nên sống động mà vẫn thanh lịch.
5.2. Biển hiệu và cảnh báo giao thông
Biển báo giao thông có hình thoi
Một số loại biển báo, đặc biệt là các biển cảnh báo nguy hiểm, sử dụng hình dạng hình thoi để thu hút sự chú ý của người tham gia giao thông. Tính đối xứng của hình thoi giúp tín hiệu dễ nhận diện từ nhiều hướng, nâng cao hiệu quả an toàn.
5.3. Cơ khí và thiết kế kỹ thuật
Trong một số thiết kế cơ khí, tính chất hình thoi được sử dụng như một giải pháp giúp phân bổ lực đồng đều, hạn chế sự mất cân bằng ở các điểm tiếp xúc. Điều này đặc biệt hữu ích trong các chi tiết chuyển động, nơi yêu cầu tính ổn định và độ bền cao.
5.4. Ứng dụng trong thời trang và nghệ thuật
Họa tiết hình thoi xuất hiện phổ biến trong thiết kế vải vóc, từ trang phục dân tộc đến thời trang hiện đại. Sự linh hoạt của tính chất hình thoi cho phép phối màu dễ dàng, tạo nên hiệu ứng thị giác nổi bật, mạnh mẽ và thường mang tính biểu tượng về sự vững chắc, cân đối.
Hình thoi không chỉ là một kiến thức cơ bản trong chương trình toán học, mà còn là hình mẫu tiêu biểu của sự cân đối và ứng dụng linh hoạt trong đời sống. Từ công thức tính diện tích dễ nhớ cho đến vai trò trong thiết kế, kỹ thuật và nghệ thuật, hình thoi chứng minh rằng hình học không chỉ tồn tại trên giấy, mà còn đóng vai trò quan trọng trong cách con người xây dựng và cảm nhận thế giới.
Việc hiểu rõ và vận dụng thành thạo các tính chất cũng như công thức liên quan đến hình thoi sẽ giúp học sinh không chỉ học tốt môn Toán, mà còn phát triển tư duy phân tích và ứng dụng sáng tạo trong thực tế.
>> Tham khảo: Bồn rửa mắt khẩn cấp giá rẻ