Đường cao tam giác đều
Trong chương trình hình học cơ bản và nâng cao, đường cao tam giác đều không chỉ là một yếu tố hình học đơn thuần mà còn là công cụ then chốt để giải quyết nhiều bài toán liên quan đến diện tích, khoảng cách, trọng tâm hay ứng dụng trong mô hình không gian. Việc nắm rõ bản chất, cách dựng và các tính chất của đường cao trong tam giác đều giúp học sinh không chỉ giải nhanh các bài tập mà còn rèn luyện tư duy logic và hình dung không gian tốt hơn. Bài viết này sẽ giúp bạn tìm hiểu sâu hơn về khái niệm này qua cách tiếp cận dễ hiểu, ứng dụng thực tiễn và mở rộng kiến thức.
Đường cao trong tam giác nói chung là đoạn thẳng kẻ từ một đỉnh, vuông góc với cạnh đối diện (hay cạnh đáy). Trong tam giác đều – tức là tam giác có ba cạnh bằng nhau và ba góc bằng nhau (đều bằng 60 độ), mang những tính chất riêng biệt vượt trội so với các loại tam giác thông thường
Cụ thể, trong tam giác đều, ba đường cao trùng với ba đường trung tuyến, đường phân giác và đường trung trực.Chỉ trong tam giác đều mới xuất hiện đặc điểm này, nơi đường cao không chỉ đơn giản là đoạn thẳng vuông góc mà còn đóng vai trò như một trục đối xứng hoàn chỉnh, thể hiện sự cân bằng tuyệt đối trong cấu trúc hình học.
Cách vẽ đường cao trong tam giác đều
Để dựng được, bạn cần thực hiện các bước sau:
Vẽ tam giác đều ABC với độ dài ba cạnh bằng nhau.
Từ đỉnh A, kẻ một đoạn thẳng vuông góc với cạnh BC. Đoạn thẳng này cắt BC tại điểm H.
AH chính là đường cao trong tam giác đều xuất phát từ đỉnh A.
Tương tự, ta có thể kẻ các đường cao xuất phát từ đỉnh B và đỉnh C.
Cả ba đường cao này sẽ cắt nhau tại cùng một điểm, được gọi là trọng tâm G của tam giác.
>> Tham khảo: Tính chất hình thoi
Trong tam giác bất kỳ, đường cao chủ yếu được sử dụng để hỗ trợ tính diện tích hoặc xác định góc vuông.
Tuy nhiên, đối với tam giác đều, đường cao đảm nhận nhiều chức năng quan trọng hơn.
Bằng nhau: Cả ba đường cao có độ dài bằng nhau do tam giác đều có ba cạnh và ba góc bằng nhau.
Đồng quy tại một điểm: Ba đường cao giao nhau tại đúng trọng tâm của tam giác.
Chia đôi đáy: Mỗi đường cao chia cạnh đối diện thành hai đoạn bằng nhau.
Góc vuông tại chân đường cao: Giao điểm giữa đường cao và cạnh đối diện tạo thành một góc vuông (90 độ).
Là đường trung tuyến và phân giác: Trong tam giác đều, mỗi đường cao đồng thời là trung tuyến (nối đỉnh với trung điểm cạnh đối diện) và phân giác (chia đôi góc tại đỉnh).
Chính vì thế, việc hiểu rõ tính chất của đường cao này sẽ giúp học sinh xử lý các dạng bài liên quan một cách chính xác và nhanh chóng.
Đường cao đóng vai trò cực kỳ quan trọng trong tính diện tích tam giác. Đối với tam giác đều cạnh a, chiều cao (ký hiệu là h) được tính bằng công thức:
h = (a × √3) / 2
Công thức này được suy ra từ định lý Pythagoras, khi chia tam giác đều thành hai tam giác vuông. Chiều cao cũng có thể được dùng trong nhiều công thức khác như tính bán kính đường tròn nội tiếp, ngoại tiếp, hay tìm tọa độ trọng tâm trong hệ trục tọa độ.
Trong thế giới hình học, đường cao tam giác đều không chỉ là một khái niệm cơ bản mà còn là yếu tố mở đầu cho hàng loạt ứng dụng sâu rộng, từ các bài toán học sinh tiểu học đến các phân tích kỹ thuật cao cấp trong thực tế đời sống. Với đặc tính độc đáo là trùng với trung tuyến và phân giác, đường cao trong tam giác đều trở thành một công cụ mạnh mẽ giúp đơn giản hóa và tối ưu hóa quá trình giải toán cũng như thiết kế trong kỹ thuật và nghệ thuật.
Tính nhanh diện tích: Đường cao là công cụ quen thuộc giúp học sinh áp dụng trực tiếp công thức diện tích một cách hiệu quả.
Trong tam giác đều, chiều cao cũng là trục đối xứng, nên mọi yếu tố trở nên cân bằng và dễ thao tác.
Xác định trọng tâm chính xác
Đường cao này giúp xác định trọng tâm chính xác
Khi làm việc với các bài toán tọa độ, việc dựng đường cao từ một đỉnh xuống cạnh đối diện giúp học sinh xác định giao điểm – chính là chân đường cao. Từ đây, có thể tính tọa độ trọng tâm một cách dễ dàng bằng cách trung bình cộng tọa độ ba đỉnh tam giác.
Tối ưu hóa trong bài toán cực trị
Nhiều bài toán yêu cầu tìm độ dài ngắn nhất, khoảng cách ngắn nhất từ điểm đến đường thẳng hoặc tối ưu hóa diện tích – tất cả đều có thể được giải quyết hiệu quả thông qua việc vận dụng kiến thức về đường cao này
Công cụ hỗ trợ chứng minh hình học
Trong các bài toán chứng minh đồng quy, đẳng giác, hoặc chia đều vùng tam giác, đường cao giúp không gian hình học trở nên rõ ràng hơn nhờ việc phân tích, qua đó giúp học sinh dễ dàng xác định các điểm đặc trưng như trực tâm, trọng tâm hay tâm của đường tròn nội tiếp.
Không chỉ gói gọn trong sách vở, nó còn góp mặt trong nhiều lĩnh vực thực tiễn:
Trong kiến trúc: Thiết kế mái nhà hình tam giác hay cấu trúc mặt cắt có dạng hình học cân đối đều dựa trên nguyên lý của tam giác đều và đường cao để đảm bảo độ ổn định cũng như tính thẩm mỹ.
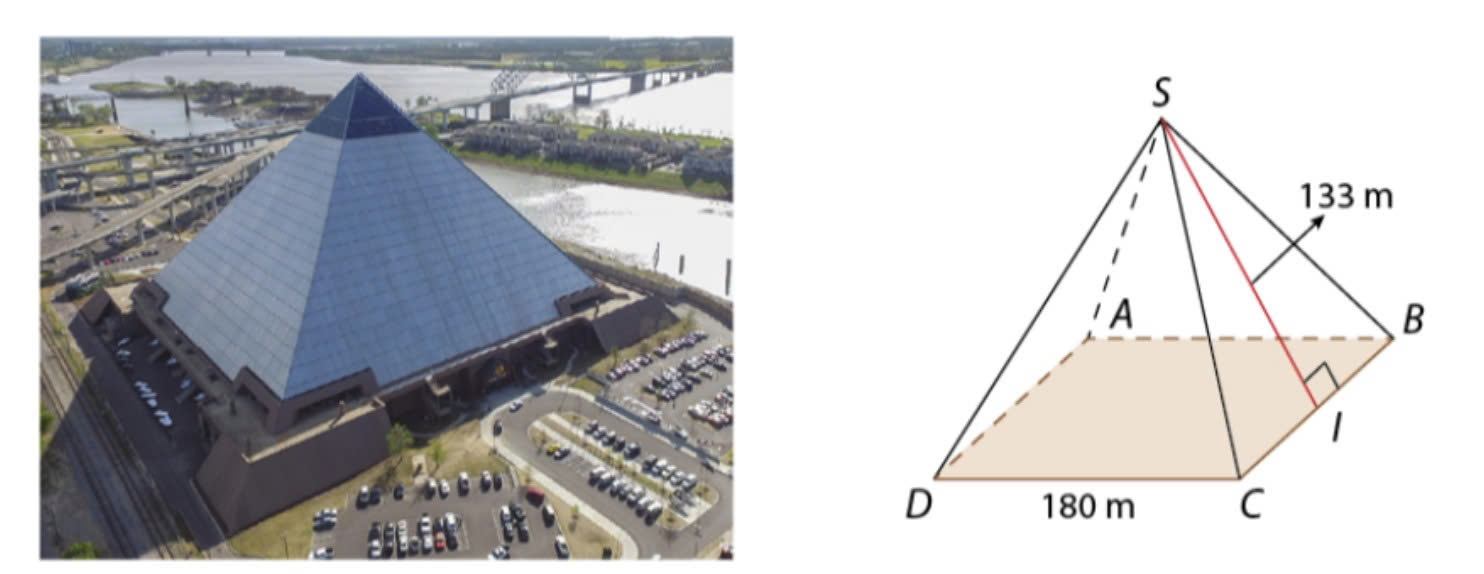
Ứng dụng trong kiến trúc
Trong kỹ thuật xây dựng: Khi phân tích lực hoặc mô hình hóa các khung kết cấu, các kỹ sư thường dùng đường cao này để xác định trục cân bằng, giúp phân bổ lực đều đặn, tránh lệch tâm và mất ổn định.
Trong mỹ thuật và thiết kế đồ họa: Việc sử dụng đường cao để tạo bố cục đối xứng giúp sản phẩm trực quan hơn, cân bằng thị giác và thu hút người xem – từ logo đến thiết kế không gian nội thất.
Ngoài ra, nó còn hỗ trợ phát triển tư duy đại số – yếu tố cốt lõi trong các kỳ thi toán học nâng cao và những lĩnh vực kỹ thuật ứng dụng cao.
Khi học sinh tiếp cận và giải các bài toán liên quan đến đường cao của tam giác đều, không ít bạn dễ gặp phải những lỗi thường xuyên lặp lại, chẳng hạn như:
- Nhầm giữa đường cao và trung tuyến: Ở tam giác đều, hai đoạn thẳng này trùng nhau cả về độ dài lẫn vị trí. Tuy nhiên, nếu áp dụng đặc điểm đó cho các tam giác không đều thì rất dễ dẫn đến sai lầm trong lập luận hình học.
- Sử dụng sai định lý Pythagore: Một số học sinh không nhận ra rằng đường cao trong tam giác đều chia cạnh đáy thành hai phần bằng nhau. Việc bỏ sót chi tiết này khiến quá trình thay số vào công thức trở nên thiếu chính xác và dễ dẫn đến kết quả sai.
- Xác định sai góc vuông tại chân đường cao: Nếu điểm đặt vuông góc không rõ ràng hoặc bị lệch vị trí, toàn bộ quá trình chứng minh hình học có thể bị phá vỡ.
- Bỏ qua tính chất đối xứng của tam giác đều: Đường cao còn đóng vai trò là trục đối xứng của hình. Việc không tận dụng điều này có thể khiến cách giải trở nên dài dòng và phức tạp hơn mức cần thiết.
Giải pháp khắc phục
Thường xuyên luyện tập các bài toán liên quan đến đường cao trong tam giác đều, kết hợp với thói quen vẽ hình cẩn thận và ghi nhớ các đặc điểm hình học đặc biệt, sẽ giúp học sinh hạn chế những sai sót không đáng có và nâng cao hiệu quả tư duy trong quá trình học tập.