Đường cao tam giác đều​

1. Đường cao tam giác đều là gì?

Trong hình học, tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau, mỗi góc đều bằng 60 độ. Đường cao của tam giác đều là đoạn thẳng kẻ từ một đỉnh vuông góc xuống cạnh đối diện (còn gọi là đáy).

Điểm đặc biệt của tam giác đều so với các tam giác khác là mỗi đường cao đồng thời cũng là đường phân giác, đường trung tuyến và đường trung trực. Nói cách khác, ba đường cao của tam giác đều vừa bằng nhau, vừa cắt nhau tại cùng một điểm, gọi là tâm của tam giác đều.

Ngoài ra, độ dài đường cao của tam giác đều có thể tính nhanh bằng công thức:

h=(a × √ 3) / 2

Trong đó:

a là độ dài cạnh của tam giác đều.

h là độ dài đường cao.

Ví dụ: Nếu tam giác đều có cạnh dài 6 cm, thì đường cao sẽ là:

h=(6 × √ 3) / 2 ≈ 5, 2 cm.

Đường cao tam giác đều không chỉ giúp tính diện tích mà còn thể hiện sự đặc biệt của tam giác đều khi vừa là đường trung tuyến, phân giác và trung trực. Đây là điểm khiến tam giác đều trở thành một trong những hình đặc biệt và cân đối nhất trong hình học.

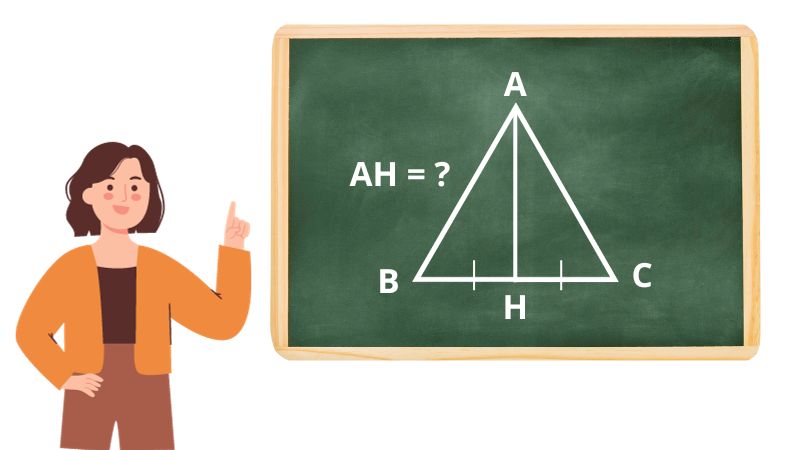Đường cao trong tam giác đều

2. Công thức tính đường cao tam giác đều

Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau (mỗi góc 60 độ). Trong tam giác đều, ba đường cao cũng bằng nhau, đồng thời là đường trung tuyến, đường trung trực và phân giác.

Để tính độ dài đường cao của tam giác đều, bạn chỉ cần nhớ công thức:

h=(a × √ 3) / 2

Trong đó:

a là độ dài cạnh của tam giác đều

h là độ dài đường cao kẻ từ một đỉnh xuống cạnh đối diện

Công thức này xuất phát từ việc tam giác đều có thể chia thành hai tam giác vuông bằng nhau, trong đó đường cao là cạnh đối diện góc 60 độ.

Ví dụ minh họa:

Nếu tam giác đều có độ dài cạnh là 8 cm, thì đường cao sẽ là:

h=(8 × √ 3) / 2 ≈ 6, 93 cm.

Nhờ công thức này, bạn có thể dễ dàng tính diện tích tam giác đều bằng cách:

S=(a × h) / 2

hoặc áp dụng công thức trực tiếp:

S=(a² × √ 3) / 4

Chỉ cần nhớ: đường cao tam giác đều=(cạnh nhân căn 3) chia 2. Đây là công thức cơ bản nhưng rất hữu ích khi tính toán nhanh trong học tập và thực tế.

Tam giác đều

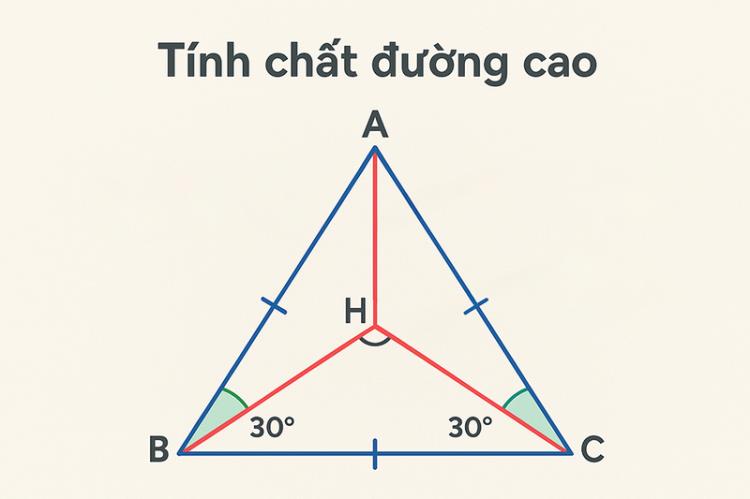3. Ứng dụng của tam giác đều

Đường cao của tam giác đều không chỉ là kiến thức hình học cơ bản mà còn mang nhiều ứng dụng thực tế và ý nghĩa trong học tập, thiết kế và cuộc sống.

Tính diện tích nhanh và chính xác

Một trong những ứng dụng quan trọng nhất là giúp tính diện tích tam giác đều. Khi biết cạnh, chỉ cần tính đường cao bằng công thức h=(a × √ 3) / 2, sau đó áp dụng công thức S=(a × h) / 2 để ra kết quả nhanh chóng.

Xác định tâm của tam giác đều

Trong tam giác đều, ba đường cao cắt nhau tại một điểm duy nhất, và điểm đó cũng chính là tâm đường tròn nội tiếp và ngoại tiếp của tam giác. Nhờ đó, đường cao giúp xác định vị trí cân đối và đối xứng của tam giác.

Thiết kế, xây dựng và trang trí

Hình tam giác đều và đường cao thường được ứng dụng để chia đều diện tích hoặc xác định điểm đặt trụ, cột, hoặc chi tiết đối xứng trong kiến trúc, nội thất. Trong đồ họa hoặc thiết kế hoa văn, đường cao giúp chia hình tam giác đều thành các phần cân đối, đẹp mắt.

Giúp phân tích và chứng minh hình học

Trong các bài toán chứng minh,tam giác đều là công cụ quan trọng để chứng minh các tính chất như sự cân đối, tính chất trung tuyến, phân giác và trung trực trùng nhau.

Tính toán trong các ngành kỹ thuật

Đường cao của tam giác đều còn xuất hiện trong tính toán kết cấu, thiết kế cơ khí, các mô hình lưới tam giác trong đồ họa máy tính hay thiết kế các chi tiết máy có dạng hình học đặc biệt.

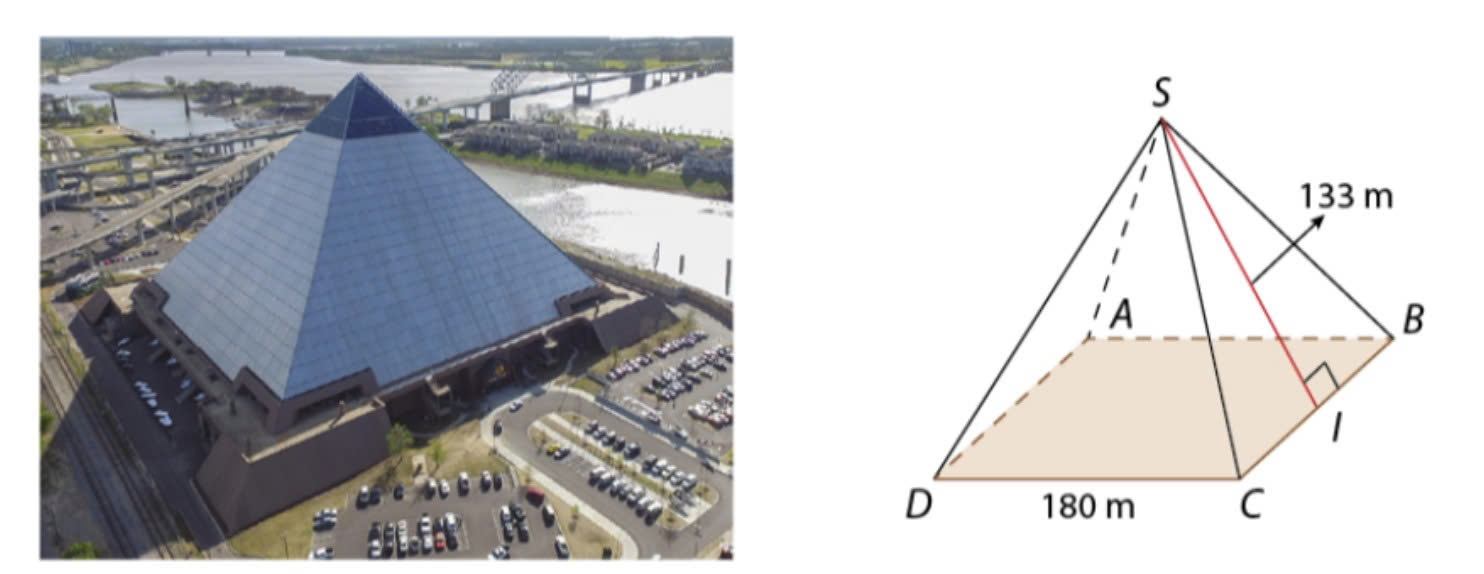Ứng dụng trong kiến trúc

4. Mẹo ghi nhớ công thức tam giác đều

Công thức tính tam giác đều khá ngắn gọn:

h=(a × √ 3) / 2

Trong đó, a là độ dài cạnh của tam giác đều. Tuy nhiên, để không bị nhầm lẫn và dễ nhớ hơn, bạn có thể áp dụng một vài mẹo sau.

Nhớ câu “ cạnh nhân căn ba chia hai”

Chỉ cần đọc thành câu: cạnh nhân căn ba chia hai là đủ để nhớ thứ tự phép tính và tránh bỏ sót căn bậc hai.

Liên tưởng hình học

Hãy tưởng tượng tam giác đều được chia thành hai tam giác vuông bằng cách kẻ đường cao. Lúc này, đường cao đóng vai trò là cạnh đối diện góc 60 độ, nên độ dài của nó sẽ là: cạnh × sin 60° =a × √ 3 / 2.

Ghi chú lên hình vẽ

Khi học hoặc làm bài tập, vẽ nhanh một tam giác đều, đánh dấu cạnh, đường cao và viết công thức ngay bên cạnh. Cách này giúp não bộ liên kết công thức với hình ảnh trực quan, ghi nhớ lâu hơn.

Ôn lại bằng ví dụ số

Thay vì chỉ học công thức khô khan, hãy thử tự tính đường cao với cạnh cụ thể, ví dụ: cạnh 4 cm, 6 cm hoặc 10 cm. Sau vài lần tính, công thức sẽ trở nên quen thuộc và tự nhiên hơn.

Chỉ cần nhớ “ cạnh nhân căn ba chia hai” và liên kết công thức với hình vẽ cụ thể, bạn sẽ dễ dàng ghi nhớ công thức tam giác đều và áp dụng chính xác khi cần.