Công thức đạo hàm logarit
Đạo hàm logarit, một khái niệm quan trọng trong toán học và giải tích, có một lịch sử phát triển phong phú gắn liền với sự tiến bộ của toán học qua nhiều thế kỷ. Dưới đây là một tóm tắt về lịch sử ra đời của đạo hàm logarit:
1. Sự phát triển ban đầu của logarit
Logarit được giới thiệu lần đầu bởi nhà toán học người Scotland John Napier vào năm 1614. Mục đích của ông là đơn giản hóa các phép tính nhân và chia phức tạp thành các phép cộng và trừ dễ dàng hơn. Sau đó, Henry Briggs, một nhà toán học người Anh, đã cải tiến hệ thống logarit của Napier và đưa ra bảng logarit cơ số 10, còn gọi là logarit thập phân, vào năm 1624.
2. Hình thành khái niệm đạo hàm
Khái niệm đạo hàm được phát triển vào thế kỷ 17 bởi Isaac Newton và Gottfried Wilhelm Leibniz, hai nhà toán học lớn của thời kỳ này. Đạo hàm là một công cụ quan trọng trong giải tích, cho phép tính tốc độ thay đổi của một hàm số tại một điểm bất kỳ.
>> Tham khảo: Công thức cấp số cộng cấp số nhân
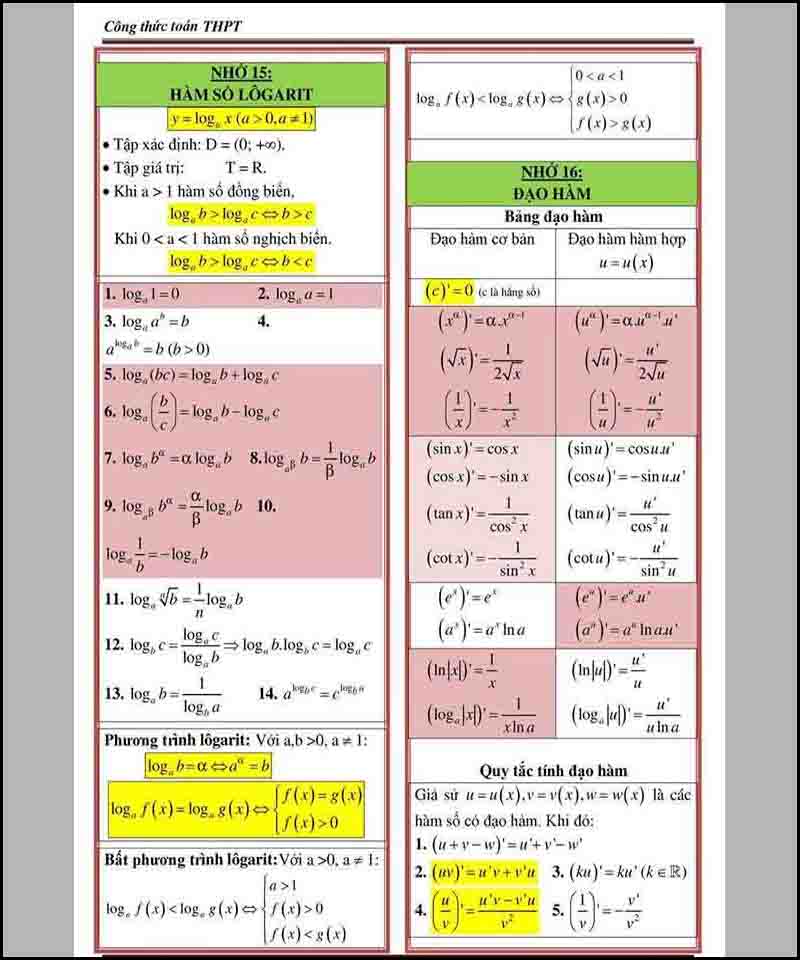
Đạo hàm logarit
3. Đạo hàm của hàm số logarit
Đạo hàm của hàm logarit tự nhiên (ln(x)) được phát hiện và chứng minh trong bối cảnh phát triển của giải tích. Các nhà toán học đã sử dụng định nghĩa đạo hàm và các quy tắc cơ bản của giải tích để tìm ra công thức đạo hàm của hàm logarit. Kết quả là:
Đạo hàm này có vai trò quan trọng trong nhiều ứng dụng toán học và khoa học.
Tham khảo: thiết kế website giá rẻ chuẩn seo
4. Các nhà toán học đóng góp vào sự phát triển
Các nhà toán học như Leonhard Euler cũng đóng góp quan trọng vào việc phát triển và ứng dụng các khái niệm liên quan đến logarit và đạo hàm. Euler đã mở rộng và hệ thống hóa nhiều kết quả quan trọng trong giải tích và toán học nói chung.
Tóm tắt
1614: John Napier giới thiệu logarit.
1624: Henry Briggs cải tiến và đưa ra logarit thập phân.
Thế kỷ 17: Isaac Newton và Gottfried Wilhelm Leibniz phát triển khái niệm đạo hàm.
Đạo hàm của logarit tự nhiên được tìm ra và chứng minh trong bối cảnh phát triển giải tích, với đóng góp quan trọng của nhiều nhà toán học như Leonhard Euler.
Khái niệm đạo hàm logarit đã trở thành một phần quan trọng trong toán học hiện đại, với ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau từ khoa học tự nhiên đến kỹ thuật và kinh tế
Tham khảo: Công ty dịch vụ marketing
Công thức
Đạo hàm logarit có nhiều ứng dụng trong đời sống và các lĩnh vực khoa học, kỹ thuật, và kinh tế. Dưới đây là một số ví dụ cụ thể về các ứng dụng của đạo hàm logarit trong đời sống:
1. Kinh tế và tài chính
Tăng trưởng liên tục và lãi suất
Mô hình tăng trưởng liên tục: Trong kinh tế, mô hình tăng trưởng liên tục được sử dụng để mô tả tăng trưởng kinh tế hoặc sự tăng trưởng của đầu tư. Đạo hàm logarit giúp phân tích tốc độ tăng trưởng liên tục của một biến số kinh tế.
Lãi suất liên tục: Lãi suất liên tục (continuously compounded interest) được tính bằng cách sử dụng logarit tự nhiên. Đạo hàm logarit giúp xác định tỷ lệ thay đổi liên tục của vốn đầu tư theo thời gian.
2. Sinh học và y học
Tốc độ tăng trưởng của vi khuẩn và tế bào
Mô hình tăng trưởng vi khuẩn: Trong sinh học, logarit và đạo hàm logarit được sử dụng để phân tích tốc độ tăng trưởng của vi khuẩn hoặc tế bào. Sự tăng trưởng này thường tuân theo quy luật hàm mũ, và logarit giúp chuyển đổi dữ liệu để dễ dàng phân tích.
Dược động học: Trong y học, đạo hàm logarit được sử dụng để mô tả tốc độ phân hủy thuốc trong cơ thể. Các mô hình này giúp tối ưu hóa liều lượng và thời gian dùng thuốc.
3. Khoa học môi trường
Phân tích nồng độ chất ô nhiễm
Biến đổi logarit: Trong phân tích nồng độ chất ô nhiễm trong môi trường, sử dụng logarit giúp làm mượt dữ liệu và dễ dàng hơn trong việc phân tích. Đạo hàm logarit cho phép xác định tốc độ thay đổi nồng độ chất ô nhiễm theo thời gian.
4. Kỹ thuật
Điều khiển tự động và mô hình hóa hệ thống
Điều khiển tự động: Đạo hàm logarit được sử dụng trong các hệ thống điều khiển tự động để phân tích và thiết kế hệ thống phản hồi. Nó giúp mô tả sự thay đổi tỷ lệ của các tín hiệu điều khiển và đầu ra.
Mô hình hóa hệ thống: Trong kỹ thuật, đặc biệt là kỹ thuật điện và điện tử, logarit và đạo hàm logarit được sử dụng để mô hình hóa hệ thống và phân tích các tín hiệu.
5. Truyền thông
Thang đo dB (decibel)
Âm thanh và tín hiệu: Đạo hàm logarit được sử dụng trong tính toán thang đo decibel (dB) trong âm thanh và viễn thông. Thang đo dB là một thang đo logarit, giúp mô tả tỷ lệ giữa hai mức độ cường độ âm thanh hoặc tín hiệu.
Tóm lại
Đạo hàm logarit là một công cụ quan trọng và hữu ích trong nhiều lĩnh vực khác nhau của đời sống. Từ kinh tế, sinh học, khoa học môi trường đến kỹ thuật và truyền thông, đạo hàm logarit giúp phân tích và hiểu rõ hơn về các quá trình và hệ thống phức tạp.
Tham khảo: Thực đơn giảm cân cho nữ cơ địa khó giảm
Đạo hàm logarit, như một phần của giải tích, không phải do một cá nhân duy nhất phát minh ra, mà là kết quả của sự phát triển và đóng góp từ nhiều nhà toán học nổi tiếng trong lịch sử. Tuy nhiên, có những cá nhân quan trọng đã góp phần đáng kể vào việc phát triển khái niệm này. Dưới đây là một số nhà toán học có ảnh hưởng lớn đến sự phát minh và phát triển của đạo hàm logarit:
1. John Napier (1550-1617)
Đóng góp: John Napier, một nhà toán học người Scotland, là người đầu tiên giới thiệu logarit vào năm 1614. Mặc dù ông không phát minh ra đạo hàm logarit, công trình của ông về logarit đã đặt nền móng cho sự phát triển sau này của các khái niệm liên quan.

John Napier
2. Isaac Newton (1643-1727) và Gottfried Wilhelm Leibniz (1646-1716)
Đóng góp: Cả Isaac Newton và Gottfried Wilhelm Leibniz đều được công nhận là những người sáng lập giải tích, một lĩnh vực toán học mà trong đó khái niệm đạo hàm được phát triển. Cả hai nhà toán học này đều độc lập phát triển các nguyên tắc cơ bản của đạo hàm trong những năm cuối thế kỷ 17.
Cụ thể: Họ đã xây dựng các quy tắc cơ bản của giải tích, trong đó có việc tính đạo hàm của hàm số logarit.
3. Johann Bernoulli (1667-1748)
Đóng góp: Johann Bernoulli, một thành viên của gia đình Bernoulli nổi tiếng trong toán học, đã đóng góp nhiều cho giải tích và cụ thể là trong việc sử dụng logarit trong các bài toán đạo hàm. Ông là một trong những người đầu tiên sử dụng và giảng dạy về giải tích, bao gồm cả việc tính đạo hàm của các hàm logarit.
4. Leonhard Euler (1707-1783)
Đóng góp: Leonhard Euler là một nhà toán học người Thụy Sĩ đã có nhiều đóng góp quan trọng cho giải tích và lý thuyết hàm số. Euler đã phát triển và hệ thống hóa nhiều khái niệm liên quan đến logarit và đạo hàm. Ông cũng là người đã giúp phổ biến và mở rộng các khái niệm này qua các công trình toán học của mình.
5. Pierre-Simon Laplace (1749-1827)
Đóng góp: Pierre-Simon Laplace, một nhà toán học và nhà thiên văn học người Pháp, đã sử dụng logarit và đạo hàm logarit trong nhiều nghiên cứu về xác suất và thống kê. Công trình của ông đã mở rộng ứng dụng của đạo hàm logarit trong các lĩnh vực này.
Tổng kết
Sự phát triển của đạo hàm logarit là một quá trình kéo dài qua nhiều thế kỷ với sự đóng góp của nhiều nhà toán học nổi tiếng. Mặc dù John Napier là người đầu tiên giới thiệu khái niệm logarit, các nhà toán học như Isaac Newton, Gottfried Wilhelm Leibniz, Johann Bernoulli, Leonhard Euler, và Pierre-Simon Laplace đã phát triển và hoàn thiện khái niệm đạo hàm logarit, biến nó thành một phần quan trọng của giải tích và toán học hiện đại.
Cách làm các dạng bài tập Logarit
Dạng 1: So sánh các biểu thức chứa Logarit tự nhiên: Để giải bài tập so sánh các biểu thức có chứa Logarit, ta thực hiện theo các bước sau:
Áp dụng các tính chất của Logarit và Logarit tự nhiên để giản lược các biểu thức.
Tiến hành so sánh các biểu thức đã được đơn giản hóa và sử dụng một số tính chất của Logarit để hoàn thành bài tập.
Dạng 2: Biểu diễn Logarit hoặc rút gọn biểu thức chứa Logarit: Giải bài tập dạng 2 theo các bước sau:
Áp dụng các tính chất của Logarit để biến đổi các biểu thức sao cho Logarit xuất hiện theo yêu cầu của đề bài.
Thay các giá trị được cho trong đề bài vào biểu thức và thực hiện việc rút gọn theo thứ tự thực hiện các phép toán như sau:
Nếu biểu thức có dấu ngoặc: thực hiện trong ngoặc trước → lũy thừa (căn bậc n) → nhân chia, cộng trừ.
Nếu biểu thức không có dấu ngoặc: lũy thừa (căn bậc n) → nhân chia, cộng trừ.
Dạng 3: Rút gọn biểu thức Logarit: Để giải bài tập rút gọn biểu thức Logarit, thực hiện theo 2 bước sau:
Chuyển đổi các công thức Logarit về cùng một cơ số.
Rút gọn các Logarit có cùng cơ số theo nguyên tắc.
Nếu biểu thức có dấu ngoặc: thực hiện trong ngoặc trước → lũy thừa (căn bậc n) → nhân chia, cộng trừ.
Nếu biểu thức không có dấu ngoặc: lũy thừa (căn bậc n) → nhân chia, cộng trừ.

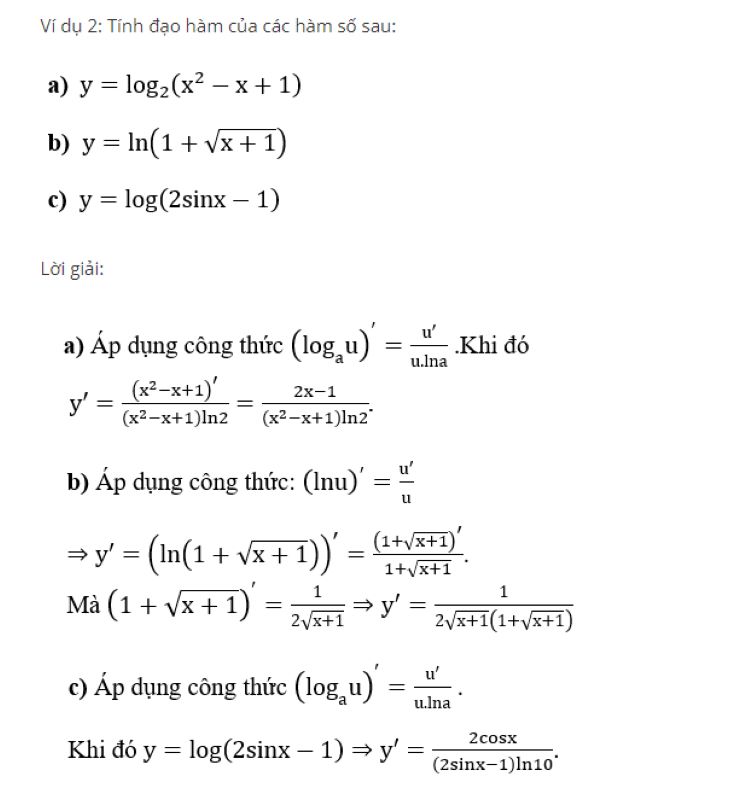

3 ví dụ cụ thể về đạo hàm lg