Công thức đạo hàm logarit
Tưởng tượng bạn đang theo dõi chiếc xe đua
Vận tốc của xe tại mỗi thời điểm chính là đạo hàm của quãng đường di chuyển theo thời gian. Nó cho bạn biết xe đang di chuyển nhanh hay chậm tại thời điểm đó.
Gia tốc - tốc độ thay đổi vận tốc - cũng được biểu diễn bằng đạo hàm thứ hai của quãng đường!
Nhưng đạo hàm không chỉ giới hạn trong chuyển động
Kinh tế: Đạo hàm giúp tính toán tốc độ tăng trưởng sản phẩm, dự đoán lợi nhuận hay mức độ rủi ro đầu tư.
Hóa học: Đạo hàm mô tả tốc độ phản ứng, giúp hiểu rõ hơn về quá trình biến đổi chất.
Vật lý: Đạo hàm được sử dụng để tính toán lực, công và cả chuyển động vật thể.
Đạo hàm tựa như siêu năng lực toán học
Phân tích sự biến đổi tinh vi của hàm số.
Dự đoán xu hướng tương lai.
Hành trình khám phá đạo hàm có thể gặp nhiều thử thách
Kiên trì và đam mê sẽ giúp bạn chinh phục kiến thức mới mẻ.
Mở ra cánh cửa đến với vô vàn ứng dụng thú vị trong toán học, khoa học và đời sống thực tiễn.

Công thức đạo hàmBạn đã bao giờ thắc mắc về bí ẩn ẩn giấu sau sức mạnh tính toán phi thường của những chiếc máy tính bỏ túi? Câu trả lời chính là logarit - phép toán kỳ diệu thu nhỏ thế giới con số khổng lồ vào tầm tay chúng ta.
Hãy tưởng tượng bạn sở hữu một chiếc hộp thần kỳ, nơi mỗi khi bạn thả vào một số dương bất kỳ, nó sẽ tiết lộ số lần bạn cần nhân số 1 với chính nó để đạt được kết quả đó. Chiếc hộp kỳ diệu này chính là phép toán logarit!
Định nghĩa
Logarit của một số x (hay còn gọi là số bị lôgarit) theo cơ số a (hay còn gọi là cơ số) là số mũ y mà khi ta nâng cơ số a lên lũy thừa y sẽ thu được số x. Ký hiệu cho phép toán này là log_a(x) = y.
Ví dụ
Logarit cơ số 10 của 100 là 2 vì 10^2 = 10 x 10 = 100.
Logarit cơ số 2 của 16 là 4 vì 2^4 = 2 x 2 x 2 x 2 = 16.
Công thức logarit
Logarit có nhiều công thức quan trọng giúp đơn giản hóa các phép toán phức tạp. Một số công thức phổ biến bao gồm:
Công thức đổi cơ số: log_a(x) = (log_b(x)) / (log_b(a)).
Công thức nhân: log_a(x * y) = log_a(x) + log_a(y).
Công thức chia: log_a(x / y) = log_a(x) - log_a(y).
Công thức lũy thừa: log_a(x^y) = y * log_a(x).
Ứng dụng của logarit
Logarit được ứng dụng rộng rãi trong nhiều lĩnh vực như:
Toán học: Giải phương trình lũy thừa và logarit, tính toán tích phân, đạo hàm.
Khoa học: Mô hình hóa các hiện tượng tăng trưởng, phân rã, tính toán độ lớn của động đất, v.v.
Kỹ thuật: Thiết kế mạch điện tử, bộ lọc tín hiệu, hệ thống điều khiển.
Kinh tế: Phân tích thị trường, tính toán lãi suất, đánh giá rủi ro đầu tư.
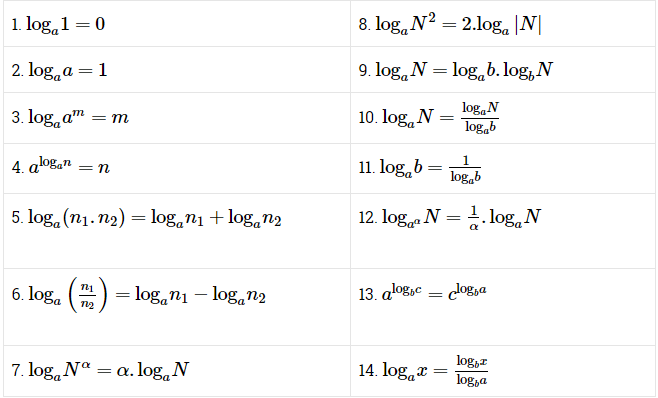
Công thức logaritĐắm chìm trong thế giới toán học bao la, ta không khỏi choáng ngợp bởi sự kết nối tinh tế giữa các khái niệm tưởng chừng như xa lạ. Một ví dụ điển hình chính của công thức đạo hàm logarit là mối liên hệ mật thiết giữa đạo hàm và logarit, hai mảnh ghép tưởng chừng đối lập lại hòa quyện hoàn hảo, mở ra cánh cửa giải mã những bài toán phức tạp của công thức đạo hàm logarit và khơi dậy niềm đam mê khám phá vô tận.
Hành trình khám phá bắt đầu với công thức đạo hàm cơ bản của hàm số logarit tự nhiên (ln(x)): d/dx(ln(x)) = 1/x. Mảnh ghép đầu tiên này hé lộ mối liên hệ tiềm ẩn giữa hai khái niệm tưởng chừng độc lập.
Tiếp nối hành trình
Tiếp theo, ta khám phá đạo hàm của hàm số mũ a^x (với a là số dương khác 1): d/dx(a^x) = ln(a) * a^x. Mảnh ghép này như sợi dây kết nối hai thế giới, mở ra cánh cửa giải mã những bài toán liên quan đến logarit và hàm mũ.
Quy tắc quyền năng
Bí ẩn tiếp theo được hé lộ bởi quy tắc đạo hàm hàm hợp, công cụ quyền năng cho phép ta tính đạo hàm của hàm số hợp, nơi nhiều hàm lồng ghép vào nhau. Áp dụng quy tắc này, ta tìm ra công thức đạo hàm của logarit cơ số bất kỳ: d/dx(log_a(x)) = 1/(x * ln(a)).
Vũ điệu ứng dụng
Công thức đạo hàm logarit không chỉ mang tính lý thuyết mà còn là chìa khóa mở ra vô vàn ứng dụng thực tiễn:
Giải mã những phương trình và bất phương trình hóc búa liên quan đến logarit.
Nghiên cứu sự biến thiên, cực trị của hàm số ẩn chứa logarit, dự đoán xu hướng phát triển trong các lĩnh vực khác nhau.
Ước tính tốc độ tăng trưởng hoặc suy giảm trong các mô hình toán học, đóng góp vào nghiên cứu khoa học và giải quyết vấn đề thực tế (ví dụ: mô hình sinh học, kinh tế).

Đạo hàm logaritTính đạo hàm bằng định nghĩa
Công thức: f'(x) = lim(h -> 0) [(f(x + h) - f(x)) / h]
Điều kiện: Hàm số f(x) phải liên tục tại x = a.
Ví dụ: Tính đạo hàm của hàm số f(x) = √x tại x = 2.
Chứng minh các đẳng thức về đạo hàm
Sử dụng: Các công thức đạo hàm đã học và các phép biến đổi toán học.
Mục đích: Chứng minh các đẳng thức về đạo hàm.
Ví dụ: Chứng minh hệ thức y'' + 2y' + 2y = 0 với y = e^sinx.
Viết phương trình tiếp tuyến khi biết tiếp điểm
Công thức: y - y_0 = f'(x_0)(x - x_0)
Giải thích: Biểu diễn đường thẳng đi qua M(x_0, y_0) và có hướng trùng với vectơ f'(x_0).
Cách áp dụng:
Xác định hoành độ x_0 của tiếp điểm.
Tính f'(x_0).
Ví dụ: Viết phương trình tiếp tuyến của đồ thị hàm số y = x^3 + 3mx^2 + (m + 1)x + 1 tại điểm có hoành độ x = -1.
Viết phương trình tiếp tuyến khi biết hệ số góc
Công thức: y - y_0 = k(x - x_0)
Giải thích: Biểu diễn đường thẳng đi qua M(x_0, y_0) và có hệ số góc k.
Cách áp dụng:
Xác định hoành độ x_0 của tiếp điểm.
Tính f'(x_0).
Xác định hệ số góc k (thường được cho gián tiếp qua các điều kiện khác của bài toán).
Ví dụ: Cho hàm số y = x^3 + 3mx^2 + (m + 1)x + 1. Tìm tiếp tuyến của đồ thị hàm số có hệ số góc nhỏ nhất.
Giải phương trình và bất phương trình có đạo hàm
Sử dụng: Đạo hàm để giải các phương trình và bất phương trình.
Phương pháp thường dùng:
Phương pháp đạo hàm
Phương pháp xét dấu đạo hàm
Phương pháp vi phân
Ví dụ: Giải phương trình f'(x) = 0 với f(x) = x^3 - 3x + 2.
Trên đây là một số thông tin về công thức đạo hàm logarit. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.